z = z^3+c
z = z^4+c
z = z^5+c
z = z^6+c
z = z^7+c
Matlab code untuk Mandelbrot Set
File 1 : Main Program
%---------------------------------copy mulai dari sini -----------------------------------------
clc
clear all
close all
% Mandelbrot Set
% Edited by Andri Husein
k = 80; % Number of iterations 100
Xr = [-2 2]; % x-axis range value
Yr = [-2 2]; % y-axis range value
Mandelbrot_plot(k,Xr,Yr)
xlabel('X-Axis','FontSize',16)
ylabel('Y-Axis','FontSize',16)
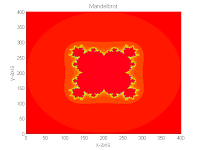
title('Mandelbrot Set','FontSize',16)
%---------------------------------copy sampai sini -------------------------------------------
File 2 : Function, simpan dengan nama: Mandelbrot_plot
%---------------------------------copy mulai dari sini -----------------------------------------
function Mandelbrot_plot(k,Xr,Yr)
n = 400;
x = linspace(Xr(1,1),Xr(1,2),n);
y = linspace(Yr(1,1),Yr(1,2),n);
[X,Y] = meshgrid(x,y);
W = zeros(length(X),length(Y));
i = sqrt(-1);
for m = 1:size(X,2)
for j = 1:size(Y,2)
[w,iter] = Mandelbrot(X(m,j)+Y(m,j)*i,k);
W(m,j) = W(m,j) + iter;
end
end
hold on;
%colormap(jet); %pilihan warna 1
%colormap(winter); %pilihan warna 2
colormap(hsv); %pilihan warna 3
%colormap(cool); %pilihan warna 4
pcolor(W); %plot 2D
caxis([0 40]); %rentang nilai warna
shading interp; %melembutkan grafik
hold off;
%-----------------------------------
function [pri,it] = Mandelbrot(c,m)
k = 0;
z = c;
while k < m
if abs(z) > 2
pri = 1;
it = k;
return;
end
% Ref http://commons.wikimedia.org/wiki/Fractal
z = z^2 + c;
%z = z^3+c;
%z = z^4+c;
%z = z^5+c;
%z = z^6+c;
%z = z^7+c;
k = k + 1;
end
pri = 0;
it = k;
%---------------------------------copy sampai sini -----------------------------------------
Copyright (c) 2006, Krzysztof Gdawiec
All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
* Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
* Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.